Geometria analityczna Natalia: Dane są trzy punkty A=(−3,−2), B=(6,4), C=(3,−3). Znajdź równanie prostej, do której należy punkt C prostopadłej do prostej AB Proszę o rozwiązanie tego zadania

Eta:

	4+2		2
Wsp. kierunkowy prostej AB: aAB=		=
	6+3		3

prosta k ⊥ pr. AB i C€ k ma równanie:

	1		3
wsp. kier. ak= −		= −
	aAB		2

	3
k: y= −		(x−xC)+yC
	2

k: y=......... dokończ......

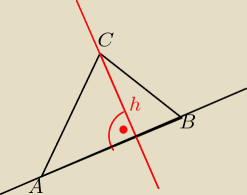
Gustlik: Jak równanie wysokości trójkata: A=(−3,−2) B=(6,4) C=(3,−3) Liczę współrzędne wektora AB^→ i współczynnik kierunkowy tej prostej: AB^→=[6−(−3), 4−(−2)]=[9, 6]

	6		2
a1=		=
	9		3

Wspólczynnik kierunkowy prostej h:

	3
a2=−		− z warunku prostopadłości
	2

	3
y=−		x+b
	2

Podstawiam wspólrzędne C

	3
−3=−		*3+b
	2

	9
−3=−		+b /*2
	2

−6=−9+2b −6+9=2b 2b=3 /:2

	3
b=
	2

	3		3
y=−		x+
	2		2

Eta:

Eta:

	3
k: y= −		*(x−3) −3
	2

	3		3
k: y= −		x +
	2		2

Eta: @Gustlik W tablicy wzorów jest wzór prostej o danym wsp. kierunkowym "a" i przechodzącej przez punkt C(x_C, y_C) k: y= a(x−x_C) +y_C i to wszystko

Gustlik: Eta, zgoda, tylko że łatwiej jest uczniowi zapamiętać równanie prostej jako kierunkowe y=ax+b bo jest to zwykła funkcja liniowa, niż jako y=a(x−x₁)+y₁. Podstawiamy a, a potem współrzędne punktu należącego do prostej i liczymy b.

Gustlik: Eta y=ax+b też jest.

Natalia: Dzięki wam, przydało mi się

Eta: Hehe

Eta: Czy wygrał ktoś z Gustlikiem ? Gustlik wie, a nawet jak nie wie, to też wie ( co uczniowi lepiej zapamiętać! )

picia: http://pl.wikipedia.org/wiki/Gustlik NIemcy nie potrafili

pigor: ... lub dla nie uznających reguł , nakazów itp. tak : A=(−3,−2) , B=(6,4) , C=(3,−3) , to AB^→=[9,6]=3[3,2] ⊥ do prostej 3x+2y+C=0 i 3*3−2*3+C=0 ⇒ C=−3 i 3x+2y−3=0 − szukana prosta w postaci ogólnej . ... i tyle −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− dużo ładniejszej od jakże "wstrętnej" postaci kierunkowej y= −³₂x+³₂ ...

Gustlik: Pigor, mi się ta metoda z wektorem prostopadłym do prostej bardzo podoba i często ją pokazuję. Problem w tym, że niestety − i tu znowu wina programu nauczania i tego idioty, który ten program napisał − nie ma tej metody w programie szkolnym. Nawet na rozszerzeniu rzadko jest ona pokazywana w szkołach, niestety w karcie wzorów maturalnych też nie ma wzorów ani na wektor równoległy ani na prostopadły do prostej. Mówię wprost − rachunek wektorowy nawet na rozszerzeniu jest traktowany po macoszemu i WIELKA SZKODA. Twój sposób fajny i chyba najszybszy, ja go znam, ale niestety − większość uczniów, nawet z rozszerzeń NIE ZNA TEGO WZORU.

Eta: https://matematykaszkolna.pl/strona/1214.html

Gustlik: Pigor co do postaci kierunkowej − nie jest ona wstrętna, jak mówisz. Np. o wiele jest ona łatwiejsza do narysowania niż ogólna, to zwykła funkcja liniowa − przeczytaj sobie tutaj − tu jest opis szybkiego rysowania wykresów funkcji liniowych − metoda geometryczna, zwana przeze mnie "schodkową". Bez żadnych obliczeń w tabelka − robi się piorunem. A z postaci ogólnej kompletnie nie widać, jak ta prosta leży − żeby narysować i tak trzeba przekształcać do kierunkowej. Łatwiej się też wyznacza proste prostopadłe i równoległe, bo są szybsze i łatwiejsze wzory. Ja osobiście wolę postać kierunkową, bo jest bardziej czytelna. Wielka szkoda, że w szkolach nie uczy się równania odcinkowego prostej:

x		y
	+		=1
a		b

Prosta taka jest niezwykle łatwa do narysowania, łatwiejsza nie tylko od postaci ogólnej, ale również od kierunkowej. Wystarczy na osi OX zaznaczyć punkt (a, 0), a na osi OY − punkt (0, b) i poprowadzić prostą. ZERO OBLICZEŃ, wykres narysowany w dwie sekundy. Zresztą na tej samej stronie też jest opis tej postaci równania prostej.

Gustlik: Pigor tu opisałem, jak szybko można narysować wykres funkcji liniowej oraz prostej danej równaniem odcinkowym − https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 . Z równania ogólnego procedura jest bardziej skomplikowana.

pigor: ... wg. mnie to urzędasy wprowadzili kretyńską jakąś tam podstawę i dziwię się nauczyciel−kom (−om) matematyki (a najbardziej tym wielkim profesorom z uczelni , którzy teraz narzekają na poziom ) , że na to się zgodzili , a nie zbojkotowali , bo ja bym się nią (podstawą) nie przejmował i tyle

pigor: ... Rozśmieszasz mnie wskazując mi jakies linki i wiedzę, że nie rozumiemy się całkowicie, ja gdybym miał narysować prostą znalaz bym sobie w pamięci 2 punkty na osiach lub nawet z postaci ogólnej wstawiając w pamięci na przemian x=0 lub y=0 , a na pewno nie sporządzał kretyńskiej tabelki i tyle . czy teraz wszyscy nauczyciele matematyki są tak upierdliwi jak TY , bo mój przez całą lekcje potrafił nie powiedzieć ani jednego słowa, tylko używał wzroku , mimiki twarzy i każdy wiedział co chce .

pigor: ... no nie zajrzałem do tego Twojego linku, ale nie miałem zamiaru czytać tego nawału informacji − przerostu formy nad treścią , a dla mnie bełkotu (bzdetów) i nie dziwię się, że młodzież zniechęca sie czymś takim do matematyki i już

Gustlik: Pigor, metoda "schodkowa" nie jest wcale skomplikowana, właśnie ja robię tym sposobem i bez tych, jak słusznie nazwałeś, kretyńskich tabelek. Poczytaj sobie, przekonasz się − zaznaczasz "b" na osi OY i lecisz o 1 w prawo i o "a" w górę, gdy a>0 lub w dół, gdy a<0, a jak a jest ułamkiem to o mianownik w prawo i o licznik w gorę, gdy a>0 lub w dół, gdy a<0. W dodatku jest zrozumiała dla uczniów, szybko sie nią robi wykres, niestety w szkołach nie jest pokazywana, mimo że występuje w niektórych podręcznikach. Ponadto metoda ta pozwala na odczytanie równania prostej z wykresu − nie raz to mi się przydało. To sie koże wydawać jak przerost formy nad treścią, ja po prostu pokazałem kilka przykładów tym sposobem, żeby lepiej zrozumieć. Ty podstawisz sobie dwa punkty, np. x=0 potem y=0 i wyznaczysz prostą, ja też tak zrobię, ale wielu osobom takie obliczenia, choc proste, sie mylą. Teraz są takie czasy, że uczniowie w liceum maja problemy z prostymi obliczeniami, które powinni już umieć w podstawówce, np. z ułamkami, z pierwiastkami, a nagminnie ze znakami dlatego m.in. ja tłumaczę metodę graficzną. Robiąc "schodkami" uczeń się nie pomyli i zrobi szybko wykres, to się robi w 2 sekundy. Co do podstawy programowej − ŚWIĘTE SŁOWA − STAWIAM . Pisana przez urzędasa, który na lekcjach matematyki w szkołę kamieniami rzucał, na kolanie i po pijaku. Cały czas o tym trąbię na tym forum i też się tej podstawy nie trzymam.

Eta: To rzucanie grochem ..........bardziej konstruktywne ! Pozdrawiam

Trivial: Eta: Fajny rysunek!

Eta:

Basia: Można jeszcze kamienie na drodze tłuc. To też miłe zajęcie

Gustlik: Eta, Basia, Was też chyba to dotyczy. Kręte ścieżki to po prostu zniechęcanie uczniów do uczenia się matematyki, kiedy wreszcie to zrozumiecie? Kochacie długie metody − trudno, Wasz problem. Ale u licha nie krytykujcie jak ktoś chce coś pokazać prosto. Pozdrawiam